Lorentz force
What is the Lorentz force?
The Lorentz force is a magnetic force that acts between a magnetic field and a moving charge. When a charge moves vertically through a magnetic field, i.e. crosses the magnetic field lines, a force acts that is in turn perpendicular to the magnetic field and the trajectory of the charge. This is the Lorentz force. It then causes the charge to move in a circular motion. The Lorentz force was discovered by the physicist Hendrik Antoon Lorentz.Table of Contents
In principle, magnetic forces
act between moving charges.
According to Maxwell's equations,
the laws of electrodynamics,
moving charges are the cause of magnetic fields.
For example, there are magnetic forces (attractive
and repulsive forces) between the poles
(north or south pole) of different permanent magnets,
which are attributed to elementary circular currents in the material.
However, there is also a force directly on a moving charge when it moves in a magnetic field.
This is known as the Lorentz force.
The Lorentz force always acts when a charge crosses the magnetic field lines. It can, for example, cause the charge to move in a circular motion.

The Lorentz force FL
acts on moving charge carriers (blue) perpendicular to the current trajectory when they cross the magnetic field lines.
In the process, the Lorentz force acts perpendicular to the magnetic flux density B
and perpendicular to the trajectory of the charge carriers v.
If the electrons can move freely, they are forced onto a circular path.
Right-hand rule for determining the direction of the Lorentz force
The direction of the Lorentz force can be determined using the so-called right-hand rule. The rule is also known as the three-finger rule.When you hold your thumb in the trajectory direction of an imagined positive charge (i.e. for electrons opposite to the trajectory) and the index finger in the direction of the magnetic field, the middle finger will indicate the direction of the force on the moving charge carriers.

The illustration shows the right-hand rule for the cross product: If you want to know the direction of the vector v3
with v3=v1xv2,
you must hold your thumb in the direction of v1
and your index finger in the direction of v2.
The spread middle finger then points in the direction of v3
(diagram on the right).
The following applies to the Lorentz force FL: FL=qvxB.
The direction of the Lorentz force can therefore be determined by holding the thumb against (because of the minus sign in the charge e) the trajectory of the electrons with speed v
and the index finger in the direction of the magnetic flux density B
(diagram on the left).
The vertically spread middle finger then points in the direction of FL.
Where is the Lorentz force put to use?
The Lorentz force, which was named after its discoverer, the physicist Hendrik Antoon Lorentz, is utilised in many physics experiments and in some technical applications. Examples include Hall probes and teltron tubes. Below, you can find out more about these two examples.Hall probe
A Hall probe, for example, utilises the physical effect of the Lorentz force. It essentially consists of a current-carrying metal disc. If a current is applied to a metal disc that is in a magnetic field, a force acts on the electrons, forcing them to one side of the disc. The electrical voltage that is generated across the disc is proportional to the magnetic field.Teltron tube
The elementary charge per mass of the electron could be determined with the help of the so-called teltron tube. This also utilises the Lorentz force. Since the elementary charge is, in turn, accessible with other experiments, the infinitesimally small mass of the electron can ultimately be determined with the teltron tube. The value of the electron mass is significant. Without precise knowledge of the electron mass, the development of efficient semiconductor components for computer technology would not be possible.To understand the teltron tube, you first need to look at the formula for the Lorentz force \(\vec{F}_L\). It reads: \(\vec{F}_L=q\vec{v}\times\vec{B}\), where \(q\) represents the charge, i.e. a negative elementary charge -e for electrons, \(\vec{v}\) represents the trajectory of the electrons as a direction vector and \(\vec{B}\) the magnetic flux density with directional information, i.e. also as a vector. The operation \(\vec{v}\times\vec{B}\) describes the so-called cross product of two vectors.
The result of this product is again a vector that is perpendicular to the two vectors of the cross product. If you are not interested in the direction of the Lorentz force, but only in the magnitude, you can also write for the magnitude FL (without specifying the vector): FL=qvB•sinθ with the sine of the angle θ between the trajectory of the electron and the magnetic flux density B.
In the teltron tube, the electrons are emitted from a hot cathode and then accelerated. They then enter a magnetic field and can be forced into a circular path.
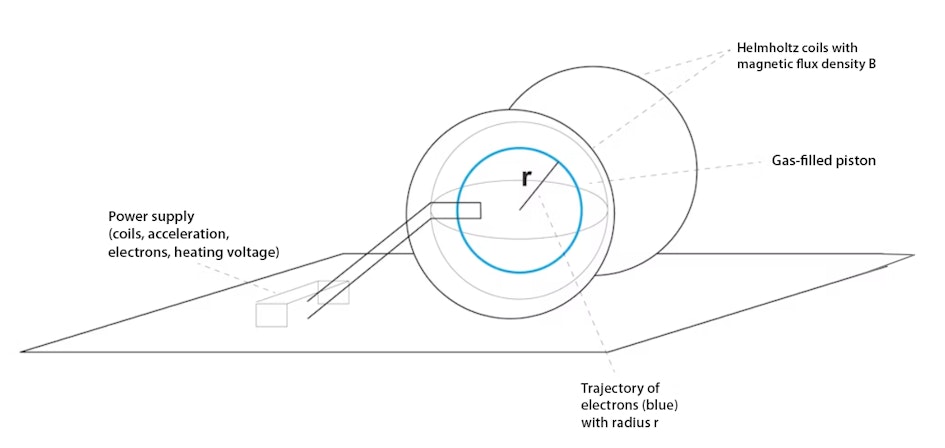
The diagram is a schematic representation of the teltron tube design.
The electrons are emitted at the hot cathode by the filament voltage and then accelerated (not shown).
The speed of the electrons can be calculated from the acceleration voltage.
However, the magnetic field between the Helmholtz coils causes the Lorentz force to act on the electrons, forcing them to follow a circular path (shown in blue).
This circular path has a radius r,
which depends on the speed of the electrons and the magnetic flux density B.
The specific charge q/m can then be calculated from B,
r
and the electron speed v.
The teltron tube is one of the fundamental experiments in physics.
The radius of the circular path r
assumes the value at which the centrifugal force \(F_z=\frac{m\cdot{v^2}}{r}\)
acting on the electrons with the mass m
and the Lorentz force \(F_L=qvB\cdot{sin\theta}\)
just compensate each other.
If the electron moves perpendicular to the magnetic field, then because sin90°=1, it follows that FL=qvB.
From Fz=FL, therefore, results:
\(\frac{m\cdot{v^2}}{r}=qvB\Rightarrow\frac{q}{m}=\frac{v^2}{rvB}=\frac{v}{rB}\)
The charge per mass of the electrons (the so-called specific electron mass) can thus be determined from the speed of the electrons, the radius of the circular path in the teltron tube and the magnitude of the magnetic flux density B.
The charge per mass of the electrons (the so-called specific electron mass) can thus be determined from the speed of the electrons, the radius of the circular path in the teltron tube and the magnitude of the magnetic flux density B.
The speed of the electrons can, in turn, be calculated from the acceleration voltage applied in the teltron tube. The magnetic flux density B can be measured using a Hall probe, for example.
Since the centrifugal force increases proportionally with the mass, but the Lorentz force increases proportionally with the charge, particles with twice the mass and twice the charge would move on the same circular path as electrons.
Therefore, only the specific elementary charge \(\frac{q}{m}\)
can be determined in the teltron tube.

Author:
Dr Franz-Josef Schmitt
Dr Franz-Josef Schmitt is a physicist and academic director of the advanced practicum in physics at Martin Luther University Halle-Wittenberg. He worked at the Technical University from 2011-2019, heading various teaching projects and the chemistry project laboratory. His research focus is time-resolved fluorescence spectroscopy in biologically active macromolecules. He is also the Managing Director of Sensoik Technologies GmbH.
Dr Franz-Josef Schmitt
Dr Franz-Josef Schmitt is a physicist and academic director of the advanced practicum in physics at Martin Luther University Halle-Wittenberg. He worked at the Technical University from 2011-2019, heading various teaching projects and the chemistry project laboratory. His research focus is time-resolved fluorescence spectroscopy in biologically active macromolecules. He is also the Managing Director of Sensoik Technologies GmbH.
The copyright for all content in this compendium (text, photos, illustrations, etc.) remains with the author, Franz-Josef Schmitt. The exclusive rights of use for this work remain with Webcraft GmbH, Switzerland (as the operator of supermagnete.it). Without the explicit permission of Webcraft GmbH, the contents of this compendium may neither be copied nor used for any other purpose. Suggestions to improve or praise for the quality of the work should be sent via e-mail to
[email protected]
© 2008-2025 Webcraft GmbH
© 2008-2025 Webcraft GmbH
