Forza di Lorentz
Che cos'è la forza di Lorentz?
La forza di Lorentz è una forza magnetica che agisce tra un campo magnetico e una carica in movimento. Se una carica si muove verticalmente attraverso un campo magnetico, cioè attraversa le linee del campo magnetico, agisce una forza che è a sua volta perpendicolare al campo magnetico e alla direzione di volo della carica. Si tratta della forza di Lorentz. Essa fa sì che la carica si muova in cerchio. La forza di Lorentz è stata scoperta dal fisico Hendrik Antoon Lorentz.Indice
In linea di principio, le forze magnetiche
agiscono tra cariche in movimento.
Secondo le equazioni di Maxwell,
le leggi dell'elettrodinamica,
le cariche in movimento sono la causa dei campi magnetici.
Ad esempio, esistono forze magnetiche (forze di attrazione
e repulsione) tra i poli
(polo nord e polo sud) di vari magneti permanenti,
che sono attribuite a correnti circolari elementari nel materiale.
Tuttavia, esiste anche una forza diretta su una carica in movimento quando questa si muove in un campo magnetico.
Si tratta della cosiddetta forza di Lorentz.
La forza di Lorentz agisce sempre quando una carica attraversa le linee del campo magnetico. Può, ad esempio, far sì che la carica descriva un movimento circolare.

La forza di Lorentz FL
agisce sui portatori di carica in movimento (blu) perpendicolarmente alla direzione di volo della corrente quando attraversano le linee del campo magnetico.
La forza di Lorentz agisce perpendicolarmente alla densità di flusso magnetico B
e perpendicolarmente alla direzione di volo dei portatori di carica v.
Se gli elettroni possono muoversi liberamente, sono costretti a seguire un percorso circolare.
Regola della mano destra per determinare la direzione della forza di Lorentz
La direzione della forza di Lorentz può essere determinata utilizzando la cosiddetta regola della mano destra. La regola è nota anche come regola delle tre dita.Se si tiene il pollice nella direzione di fuga di una carica positiva immaginaria (cioè opposta alla direzione di fuga degli elettroni) e l'indice nella direzione del campo magnetico, il dito medio indica la direzione della forza sui portatori di carica in movimento.

La figura mostra la regola della mano destra per il prodotto vettoriale: se si vuole conoscere la direzione del vettore v3
con v3=v1xv2,si deve tenere il pollice nella direzione di v1
e l'indice nella direzione di v2.
Il dito medio disteso punta quindi in direzione di v3
(figura di destra).
Per la forza di Lorentz FL
vale quanto segue: FL=qvxB.
La direzione della forza di Lorentz può quindi essere determinata tenendo il pollice contro (a causa del segno meno nella carica e) la direzione di volo degli elettroni con velocità v
e l'indice nella direzione della densità di flusso magnetico B
(figura di sinistra).
Il dito medio steso verticalmente punta quindi nella direzione FL.
Dove viene utilizzata la forza di Lorentz?
La forza di Lorentz, che prende il nome dal suo scopritore, il fisico Hendrik Antoon Lorentz, viene utilizzata in molti esperimenti fisici e in alcune applicazioni tecniche. Ad esempio, nelle sonde di Hall o nei tubi a fascio filamentoso. Qui di seguito potete trovare maggiori informazioni su questi due esempi.Sonda di Hall
Una (sonda di Hall, ad esempio, utilizza l'effetto fisico della forza di Lorentz. Consiste essenzialmente in una piastra metallica attraverso la quale scorre una corrente. Se si applica una corrente a un disco metallico che si trova in un campo magnetico, una forza agisce sugli elettroni, costringendoli a spostarsi su un lato del disco metallico. La tensione elettrica che si genera attraverso il disco è proporzionale al campo magnetico.Tubo a fascio filiforme
La carica elementare per massa dell'elettrone può essere determinata con l'aiuto del cosiddetto tubo a fascio filiforme. Anche in questo caso si utilizza la forza di Lorentz. Poiché la carica elementare è a sua volta accessibile con altri esperimenti, è possibile determinare la massa estremamente piccola dell'elettrone con il tubo a fascio filamentoso. Il valore della massa dell'elettrone è significativo. Senza una conoscenza precisa della massa dell'elettrone, lo sviluppo di componenti semiconduttori efficienti per la tecnologia informatica non sarebbe possibile.Per comprendere il tubo a fascio di filamenti, occorre innanzitutto esaminare la formula della forza di Lorentz \(\vec{F}_L\). La legge dice: \(\vec{F}_L=q\vec{v}\times\vec{B}\), dove \(q\) indica indica la carica, cioè una carica elementare negativa -e per gli elettroni, \(\vec{v}\) è la direzione di moto degli elettroni come vettore di direzione e \(\vec{B}\) è la densità di flusso magnetico con direzione, anch'essa come vettore. L'operazione \(\vec{v}\times\vec{B}\) descrive il cosiddetto prodotto vettoriale di due vettori.
Il risultato di questo prodotto è di nuovo un vettore perpendicolare ai due vettori del prodotto vettoriale . Se non si è interessati alla direzione della forza di Lorentz, ma solo alla sua grandezza, si può anche scrivere la grandezza FL (senza specificare il vettore): FL=qvB•sinθ con il seno dell'angolo θ tra la direzione di moto dell'elettrone e la densità di flusso magnetico B.
Nel tubo a fascio filiforme, gli elettroni vengono emessi da un catodo caldo e poi accelerati. Entrano quindi in un campo magnetico e possono essere costretti a seguire un percorso circolare.
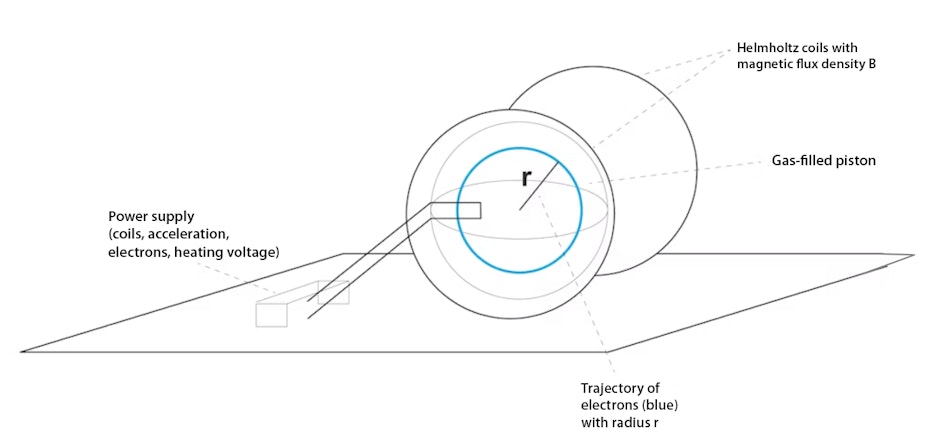
Lo schizzo mostra schematicamente la struttura di un tubo a fascio di filamenti.
Gli elettroni vengono emessi al catodo caldo dalla tensione di riscaldamento e poi accelerati (non mostrato).
La velocità degli elettroni può essere calcolata dalla tensione di accelerazione.
Tuttavia, il campo magnetico tra le bobine di Helmholtz fa sì che la forza di Lorentz agisca sugli elettroni, costringendoli a seguire un percorso circolare (in blu).
Questo percorso circolare ha un raggio r,
che dipende dalla velocità degli elettroni e dalla densità di flusso magnetico B.
Tuttavia, la cosiddetta carica specifica q/m può essere calcolata da B,
r
e dalla velocità v
degli elettroni.
Il tubo a fascio di filamenti è uno degli esperimenti fondamentali della fisica.
Il raggio del percorso circolare r
assume il valore in cui la forza centrifuga \(F_z=\frac{m\cdot{v^2}}{r}\),
che agisce sugli elettroni di massa m,
e la forza di Lorentz \(F_L=qvB\cdot{sin\theta}\)
si compensano.
Se l'elettrone vola perpendicolarmente al campo magnetico, poichè sin90°=1 vale quanto segue FL=qvB.
Ne consegue che Fz=FL:
\(\frac{m\cdot{v^2}}{r}=qvB\Rightarrow\frac{q}{m}=\frac{v^2}{rvB}=\frac{v}{rB}\)
La carica per massa degli elettroni (la cosiddetta massa specifica degli elettroni) può quindi essere determinata dalla velocità degli elettroni, dal raggio del percorso circolare nel tubo del fascio di filamenti e dall'entità della densità di flusso magnetico B.
La carica per massa degli elettroni (la cosiddetta massa specifica degli elettroni) può quindi essere determinata dalla velocità degli elettroni, dal raggio del percorso circolare nel tubo del fascio di filamenti e dall'entità della densità di flusso magnetico B.
La velocità degli elettroni può essere calcolata a sua volta dalla tensione di accelerazione applicata nel tubo a fascio di filamenti. La densità di flusso magnetico B può essere misurata, ad esempio, con una sonda di Hall.
Poiché la forza centrifuga aumenta proporzionalmente alla massa, ma la forza di Lorentz aumenta proporzionalmente alla carica, particelle con il doppio della massa e il doppio della carica volerebbero sullo stesso percorso circolare degli elettroni.
Pertanto, solo la carica elementare specifica \(\frac{q}{m}\)
può essere determinata nel tubo a fascio di filamenti.

Autore:
Dott. Franz-Josef Schmitt
Il dottor Franz-Josef Schmitt è fisico e direttore scientifico del corso pratico avanzato di fisica all'università Martin-Luther di Halle-Wittenberg. Ha lavorato alla Technische Universität di Berlino dal 2011 al 2019, dove ha diretto diversi progetti pedagogici e il laboratorio di progetti di chimica. Le sue ricerche si concentrano sulla spettroscopia di fluorescenza risolta nel tempo su macromolecole biologicamente attive. Inoltre è il direttore di Sensoik Technologies GmbH.
Dott. Franz-Josef Schmitt
Il dottor Franz-Josef Schmitt è fisico e direttore scientifico del corso pratico avanzato di fisica all'università Martin-Luther di Halle-Wittenberg. Ha lavorato alla Technische Universität di Berlino dal 2011 al 2019, dove ha diretto diversi progetti pedagogici e il laboratorio di progetti di chimica. Le sue ricerche si concentrano sulla spettroscopia di fluorescenza risolta nel tempo su macromolecole biologicamente attive. Inoltre è il direttore di Sensoik Technologies GmbH.
Il diritto d'autore sull'intero contenuto del compendio (testi, foto, illustrazioni ecc.) appartiene all'autore Franz-Josef Schmitt. I diritti esclusivi di utilizzazione dell'opera appartengono a Webcraft GmbH, Svizzera (come gestore di supermagnete.it). Senza espressa autorizzazione di Webcraft GmbH non è permesso copiarne il contenuto né utilizzarlo in alcun'altra forma. Proposte di miglioramento o complimenti riguardo al compendio possono essere inviati per e-mail a
[email protected]
© 2008-2025 Webcraft GmbH
© 2008-2025 Webcraft GmbH

