Magnetic resistance
What is meant by magnetic resistance?
Magnetic resistance is a measure of the resistance that magnetic field lines face when flowing through matter. When magnetic resistance is high, magnetic field lines have difficulty penetrating the material. The magnetic resistance is therefore inversely proportional to the magnetic permeability μ. Consequently, ferromagnetic materials have a very low magnetic resistance.Table of Contents
In magnetism,
the so-called magnetic flux
Φ
is the equivalent of the electric current I
in electricity.
Using the magnetic voltage Umag
and the magnetic flux Φ,
a magnetic resistance Rmag
can therefore be defined using the relationship:
Umag=Rmag•Φ This corresponds to Ohm's law in electricity U=R•I, where U denotes the electrical voltage, I the electrical current and R the electrical (ohmic) resistance.
In materials with high permeability, the magnetic flux is very high. The magnetic resistance is therefore very low. This applies to ferromagnetic materials such as iron.
A superconductor, on the other hand, has an infinitely large magnetic resistance. The superconductor completely displaces the magnetic flux from its interior. No magnetic field can penetrate a superconductor. The permeability of the superconductor is zero.
Example for the calculation of magnetic resistors
Using the concept of magnetic resistance, series and parallel circuits of different magnetic resistors can be calculated in the same way as in an electric circuit.For example, consider a ring-shaped coil of length L with an iron core and an air gap of width d. In this coil, the magnetic field inside the iron core is smaller than in the air gap. The field strength here is indirectly proportional to the permeability, i.e. directly proportional to the magnetic resistance. This is completely analogous to an electrical circuit. A large electric field exists at large resistors because a large voltage drop occurs across the resistor.
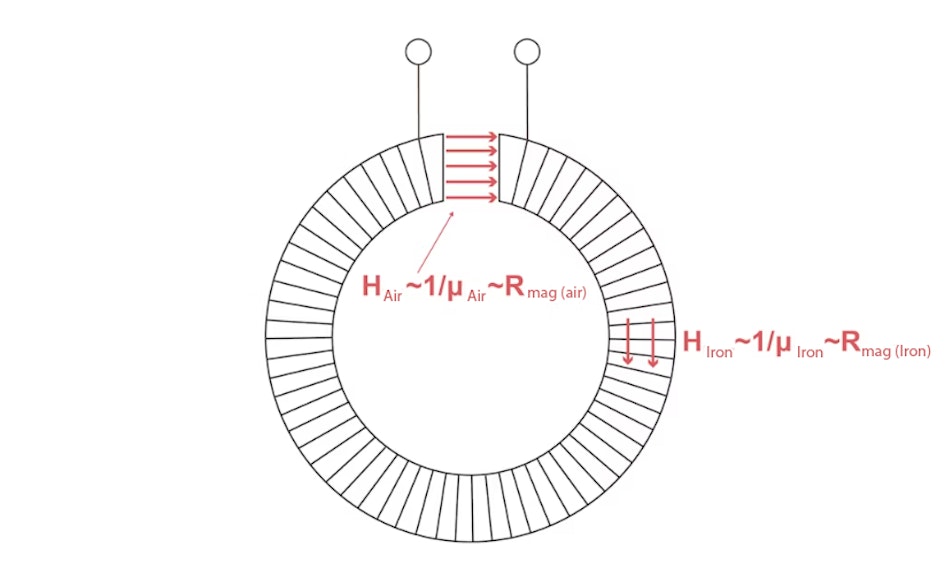
A long ring-shaped coil with an iron core represents a magnetic resistor.
An air gap also forms a magnetic resistor.
As the magnetic permeability of air is significantly lower than the permeability of iron, the magnetic resistance of the air gap is greater than the resistance of the iron core.
If the air gap is reduced, the resistance of the air gap decreases.
The magnetic voltage attributable to the air gap is, like the magnetic resistance, correspondingly large.
It is approximately the product of the magnetic field and the gap width d:
\(U_{magnetic,air gap}=H_{air}\cdot{d}=\frac{B}{\mu_0\mu_{air}}\cdot{d}\).
The magnetic voltage of the coil (with iron core), on the other hand, is:
\(U_{magnetic,coil}=H_{coil}\cdot{L}=\frac{B}{\mu_0\mu_{iron}}\cdot{L}\).
The magnetic flux is the same in the iron core and in the air gap. It runs through the cross-sectional area A and is
\(\Phi=B\cdot{A}\).
The following therefore applies to the magnetic resistance of the iron core coil:
\(R_{magnetic,coil}=\frac{U_{magnetic,coil}}{\Phi}=\frac{1}{\mu_0\mu_{iron}}\cdot\frac{L}{A}\).
While the magnetic resistance of the air gap is constituted by
\(R_{magnetic,air gap}=\frac{U_{magnetic,air gap}}{\Phi}=\frac{1}{\mu_0\mu_{air}}\cdot\frac{d}{A}\).
The "longer" an element of the magnetic series circuit is, the greater the associated magnetic resistance.
The greater the permeability μ
and the cross-sectional area of the component A,
the lower the magnetic resistance.
Just as the resistances of the components connected in series in an electrical circuit must be added together to obtain the total resistance of the circuit, the total magnetic resistance of the magnetic circuit shown is also obtained by adding the magnetic resistances of the individual components. The following therefore applies to the shown ring coil with air gap:
\(R_{magnetic}=R_{magnetic,coil}+R_{magnetic,air gap}\).
In both electrical and magnetic instances, a voltage drop across the resistors is proportional to the respective resistance.
Magnetic components could also be connected in parallel.
In this case, the magnetic resistances add up reciprocally, just like the resistances in an electrical parallel circuit.
This means that the total resistance is reduced by parallel connection compared to the individual components.

Author:
Dr Franz-Josef Schmitt
Dr Franz-Josef Schmitt is a physicist and academic director of the advanced practicum in physics at Martin Luther University Halle-Wittenberg. He worked at the Technical University from 2011-2019, heading various teaching projects and the chemistry project laboratory. His research focus is time-resolved fluorescence spectroscopy in biologically active macromolecules. He is also the Managing Director of Sensoik Technologies GmbH.
Dr Franz-Josef Schmitt
Dr Franz-Josef Schmitt is a physicist and academic director of the advanced practicum in physics at Martin Luther University Halle-Wittenberg. He worked at the Technical University from 2011-2019, heading various teaching projects and the chemistry project laboratory. His research focus is time-resolved fluorescence spectroscopy in biologically active macromolecules. He is also the Managing Director of Sensoik Technologies GmbH.
The copyright for all content in this compendium (text, photos, illustrations, etc.) remains with the author, Franz-Josef Schmitt. The exclusive rights of use for this work remain with Webcraft GmbH, Switzerland (as the operator of supermagnete.it). Without the explicit permission of Webcraft GmbH, the contents of this compendium may neither be copied nor used for any other purpose. Suggestions to improve or praise for the quality of the work should be sent via e-mail to
[email protected]
© 2008-2025 Webcraft GmbH
© 2008-2025 Webcraft GmbH
